The Importance of Viscosity in Melting

In a previous column (see Extrusion Know How, Sept. ’20), I explained how melting occurs in an extrusion (or injection) screw. It occurs by shearing or stretching the polymer with the rotation of the screw relative to the barrel. The resistance to turning the screw is how the drive energy is introduced to melt the polymer. The resistance to the screw rotation or drive power is proportional to the polymer viscosity in contact with the barrel. If you preheat the barrel before starting up, it will be coated initially with melt when screw rotation begins.

The viscosity of the polymer in contact with the barrel at a given location through which the screw turns changes continuously along the screw. The viscosity depends on the shear rate and the temperature of the polymer.

The shear rate is defined as:

γ = πDN/h, where

π = Pi,

D = diam. (in.),

N = Screw Speed (rev/sec),

h = Channel depth (in.)

The effect of the shear rate on the polymer viscosity for any particular polymer is defined by the power-law coefficient (n). The effect of temperature on the viscosity is defined by the consistency index (m). Power from shearing the polymer is termed “viscous dissipation” (e_m). It’s how most of the energy from the rotating screw changes the temperature of the polymer. Once screw rotation is started, very little energy typically enters the extruder from the barrel heaters. In fact, many extruders are run with all the heat/cool zones in cooling mode.

The calculation e_m = m(γ)¹⁺ⁿ describes viscous dissipation at any point; however, it’s true only at that point and does not consider the accumulation of energy and the corresponding rise in polymer temperature along the entire length of the screw. To do so over the length of the screw is a complex and time-consuming calculation.

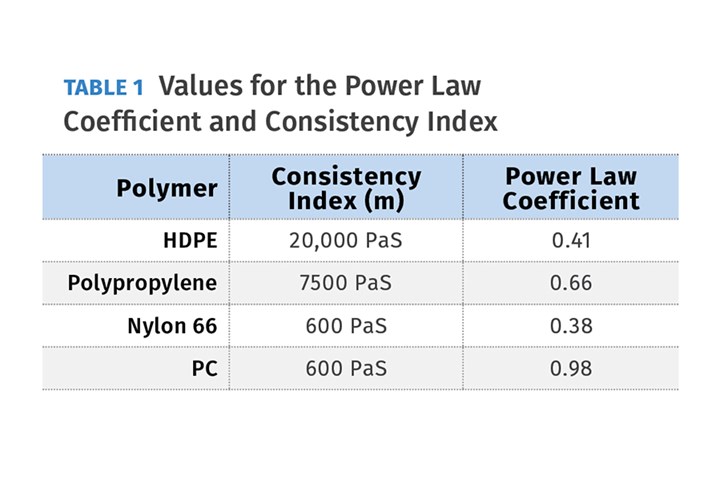
If you enter actual data into the viscous dissipation formula for four polymers (Table 1) you can see the substantial effect the viscosity has on melting. Using the same 4.5-in. screw design for each polymer and looking at the shear rate in just the metering section having a 0.350-in. depth at 100 rpm gives:

γ = π(4.5)(100÷60)÷0.350 = 67.32 sec^-1

If you put these values into the viscous dissipation calculation [e_m=m(γ)¹⁺ⁿ] the result is the shear thinning of the polymers under strain (screw rotation) and increasing temperature. The greater the viscous dissipation, the greater the power going into the polymer due to shear.

As you can see in Table 2, the polymers vary considerably in consistency index and power-law coefficient, but the combination of these is necessary to determine the power conversion. HDPE has a high consistency index, so it maintains its viscosity with increasing shear rates. Polypropylene, on the other hand, has a lower consistency index, but a higher power-law coefficient, and ends up with more viscous dissipation than HDPE and consequently would yield a similar melt temperature on the same screw because of different melt densities. To a large extent, PP’s viscous dissipation is similar to that of HDPE.   

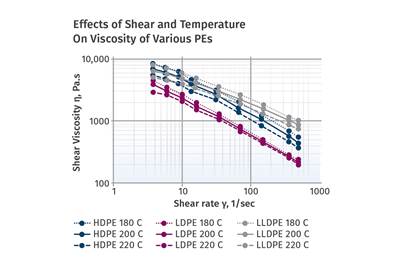
Just looking at some shear-rate/viscosity curves does not provide enough information to design a screw.

Nylon 66 is totally different and would need a much higher shear rate to match the viscous dissipation of the HDPE. PC is in a different range than nylon 66 due to its very high power-law coefficient. Nylon 66 and PC are both typically processed after drying, with consequent heating, thereby reducing the required energy and viscous dissipation. HDPE and PP are not normally processed in a dried state. That is why just looking at some shear-rate/viscosity curves does not provide enough information to design a screw.

The calculations to reach the proper melt temperature for each polymer are relatively complicated and require a desired melt temperature as a target, which can vary with every extrusion process. In addition, polymers all vary considerably in specific heat, density, crystallinity and thermal conductivity.  When you factor in the variations in the amount of melt at any point, and gain or loss from barrel heating/cooling, it makes for a complicated analysis even with very sophisticated computer simulation.

In the real world, most extrusion screws are not designed with such rigorous calculations, but as scale-ups/downs of previous designs where the power for viscous dissipation and the resultant melt temperature were previously determined. Regardless, it might be useful to have some knowledge of power-law coefficients and consistency indices to help explain the differences in screw power generation, particularly when you’re trying out a new polymer or polymer grade.

About the Author: Jim Frankland is a mechanical engineer who has been involved in all types of extrusion processing for more than 40 years. He is now president of Frankland Plastics Consulting, LLC. Contact jim.frankland@comcast.net or (724) 651-9196.